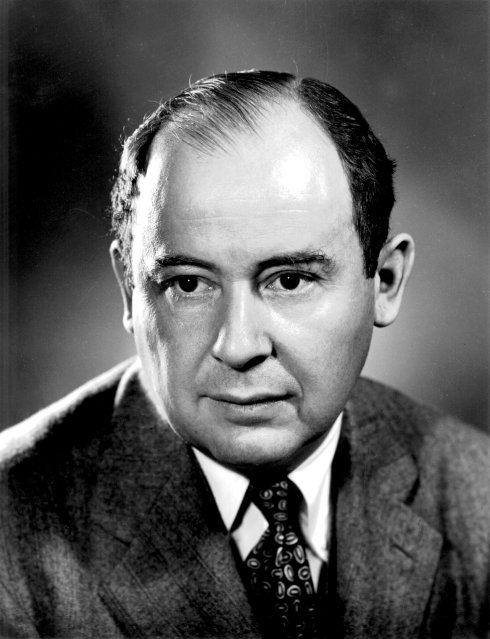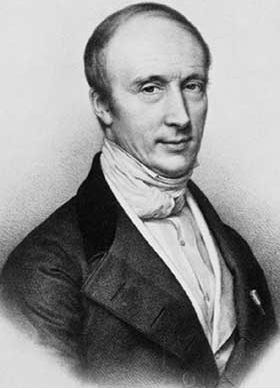A Geek's Guide to Pi: How the Most Important Number in the Universe Shapes Your Daily Life [Anniversary Edition]
🎉 Happy Pi Day! 🎉 For all my geeks out there—I spent some time last year researching the fascinating history of Pi (π) and wanted to share it again with you today.
Welcome to AI Health Uncut, a brutally honest newsletter on AI, innovation, and the state of the healthcare market. If you’d like to sign up to receive issues over email, you can do so here.
🎉 Happy Pi Day! 🎉 One of the most exciting days of the year—at least in my eyes. 😉
Did you know that:
π Each one of us uses Pi daily, without even realizing it.
π Pi is not only mentioned in the Bible but it’s also calculated there? Sure, it was a rough approximation, but still, it’s pretty amazing.
π The most famous application of π is in the Euler equation, which the amazing Richard Feynman deemed “the most remarkable formula in mathematics”.
In one of my recent joint papers, I heavily rely the Langevin Law. A notable application of the Langevin Law is Brownian Motion, a concept that was pioneered by Albert Einstein. Einstein established a relationship between the macroscopic diffusion constant and the atomic properties of matter. Our research carries significant implications for the healthcare industry, especially in reducing the risk of stroke caused by magnetic (solar) storms.

For a math geek like me, Pi Day is practically a national holiday. 😉 It’s a tribute to one of history’s most significant numbers: 3.14 and the endless digits that follow. And trust me, those extra digits aren’t just decoration—they’re crucial. Pi isn’t just important. It’s elegant, captivating, and woven into our daily lives in ways we hardly notice.
In this article, I explored the fascinating history of Pi, the epic quest to calculate its infinite decimals, and why Pi plays a starring role in machine learning. Sharing it once more, in case you missed it. 😉
1. The Fascinating History of Pi
To grasp the significance of π, let’s begin with a brief history. I won’t use any mathematical formulas in this article, which might seem a bit odd — discussing math without the equations.
Most of us recognize π as the precise (and thus elegantly simple) ratio of a circle’s circumference to its diameter. So, whenever you envision a perfect circle, π inevitably comes to mind.
History is replete with mathematicians who have found applications for π, making it impossible to name them all. However, let me mention a few notable names.
Before the concept of the circle was fully understood, there was the polygon, an inherently imperfect representation of a circle. Around 250 BC, the Greek mathematician Archimedes analyzed polygons. This polygonal approach remained dominant for over 1,000 years, earning π the nickname “Archimedes’ constant.” Archimedes calculated π’s upper and lower bounds by inscribing and circumscribing a regular hexagon around a circle and incrementally doubling the number of sides up to a 96-sided polygon. Through this method, he established that 223/71 < π < 22/7 (3.1408 < π < 3.1429).
The invention of calculus by English scientist Isaac Newton and German mathematician Gottfried Wilhelm Leibniz in the 1660s paved the way for numerous infinite series that approximate π. Newton, in 1665 or 1666, used an arcsin series to compute π to 15 decimal places, later expressing embarrassment at the extent of his calculations during a period of inactivity. Among the most celebrated infinite series is the Taylor series, named after British mathematician Brook Taylor, who introduced it in 1715. This series, which includes infinite sums of terms calculated from a function’s derivatives at a single point, has led to several π-related series, such as those for sine, tangent, and cosine, now known as the Madhava or Gregory-Leibniz series.
In 1656, British mathematician John Wallis presented the Wallis formula for π in his book “Arithmetica Infinitorum,” defining π as an infinite product of ratios of integers.
Remarkably, it wasn’t until 2015, more than 350 years later, that American mathematician Tamar Friedmann and particle physicist Carl Hagen, both at the University of Rochester, my alma mater, found a new context for the Wallis formula in quantum mechanics, specifically within the formula for the hydrogen atom’s energy states. This discovery highlighted π’s ubiquitous presence in both mathematics and science.
As mentioned earlier, π represents the ratio of a circle’s circumference to its diameter. The earliest known use of this formula was by the Welsh mathematician William Jones in 1706.
Perhaps the most famous application of π is in the Euler equation, developed by the Swiss mathematician Leonhard Euler. Often described as “the most beautiful formula in mathematics,” Euler appears never to have written it down directly, as naming conventions in mathematics can be somewhat imprecise. It is a special case of Euler’s discovery that exponential growth and circular motion are equivalent, expressed by the formula: exp(i*θ) = cos(θ) + i*sin(θ). Although π is not explicitly mentioned in this formula, it plays a crucial role in its derivation. Indeed, the arguments for cos and sin functions are functions of π. The famous American theoretical physicist Richard Feynman referred to Euler equation as “the most remarkable formula in mathematics.” In discussing cos and sin functions, Euler introduced the concept of arc length, providing a new way to represent the measure of an angle, now known as “radian measure.” For instance, 360 degrees equals 2π radians, 180 degrees is π radians, and 90 degrees equals π/2 radians. These measures, always based on a special circle with a radius of 1, underscore how cos and sin—and thus π—are vital in modeling phenomena like vibrating strings or radio waves.
The Euler equation finds applications across many science fields, particularly in fluid dynamics. Euler first presented it to the Berlin Academy in 1752. It was among the first partial differential equations documented, following the wave equation. In Euler’s original work, the equation set, including momentum and continuity equations, was underdetermined except in cases of incompressible flow. The adiabatic condition, an additional equation developed by the French mathematician Pierre-Simon Laplace in 1816, helped address this limitation.

In the latter half of the 19th century, it was established that the equation related to the balance of energy must always be maintained for compressible flows, with the adiabatic condition arising naturally from fundamental laws in cases of smooth solutions. With Albert Einstein’s introduction of the special theory of relativity, concepts like energy density, momentum density, and stress merged into the stress-energy tensor, unifying energy and momentum into the energy-momentum vector.
The fundamental equation developed by French physicist Paul Langevin, known as the Langevin Equation or Langevin Law, involves both frictional forces (which explicitly depend on π) and random forces. This equation is integral to understanding non-equilibrium systems. The fluctuation-dissipation theorem connects these forces, illustrating how they interplay within the system. Brownian Motion, which is the erratic movement of a small particle (approximately one micron in diameter) immersed in a fluid of the same density, exemplifies these principles. The study of this motion traces back to early observations by Scottish biologist Robert Brown, who noted the phenomenon in pollen grains, dust particles, and other colloidal-sized objects. The modern theory of Brownian motion took a significant leap forward with Albert Einstein, who established a relationship between the macroscopic diffusion constant and the atomic properties of matter, incorporating π as a crucial component of his formula. The application of Brownian motion theory has since expanded beyond real particles to include collective properties of macroscopic systems, such as the instantaneous concentration of any component in a chemically reacting system near thermal equilibrium.
One important area of study that has evolved from the Langevin Law is Stochastic Thermodynamics. This is a growing research area within statistical mechanics that employs stochastic variables to enhance our understanding of the non-equilibrium dynamics encountered in numerous microscopic systems. These systems include colloidal particles, biopolymers (e.g., DNA, RNA, and proteins), enzymes, and molecular motors.
The Langevin Law plays a pivotal role in my recent publication, co-authored with two colleagues, one of whom is my father. We have developed a model that delineates the interaction between a uniform magnetic field and a cylindrical ferrofluid layer. Our study holds significant implications for healthcare, aiming to mitigate the risk of stroke caused by magnetic (solar) storms. In practical terms, we propose a lightweight helmet featuring a thin ferrofluid layer that envelops the entire surface of the helmet. This invention could provide relief to approximately 6% of the global population who suffer from severe headaches due to magnetic (solar) storms, enabling them to lead normal lives.
What does the Langevin Law have to do with π? Well, π is a crucial component of this pivotal equation. Notably, π is present in the frictional term. More fundamentally, π is integral through the use of cosh, or hyperbolic cosine, which is derived from the cosine function via the Euler equation.
Named after the Polish-French physicist Marie Curie, the Curie Law represents a specific instance of the Langevin Law. It explains the magnetic susceptibility of a ferromagnet in the paramagnetic region above the Curie point. This is the temperature threshold beyond which certain materials forfeit their permanent magnetic properties.
2. The Race to Compute Decimals of Pi
Evidence exists that the Babylonians approximated π in base 60 around 1800 B.C.E., believing that π equaled 25/8, or 3.125. The ancient Egyptian scribe Ahmes, linked to the famous Rhind Papyrus, offered the approximation 256/81, which is equal to 3.16049. The Bible even provides an implicit value for π. In 1 Kings 7:23, it describes a round basin with a 30-cubit circumference and a 10-cubit diameter, implying that π equals 3 (30/10).
As humanity’s understanding of numbers evolved, so did its ability to estimate π more accurately. In the year 263, the Chinese mathematician Liu Hui asserted that π was 3.141014. Approximately 200 years later, the Indian mathematician and astronomer Aryabhata used the fraction 62,832/20,000 to approximate π as 3.1416. Around the year 1400, the Persian astronomer Jamshid al-Kashi (also known as Ghiyāth al-Dīn Jamshīd Masʿūd al-Kāshī, or al-Kāshānī) calculated π correctly to 16 digits.
In 1761, Swiss mathematician Johann Lambert demonstrated that π is an irrational number. This means it cannot be expressed as the quotient of any two whole numbers, indicating it has an infinite number of decimal places with non-repeating sequences.
Thus began the ongoing race to calculate π to the highest number of decimal places…
German theoretical physicist Jörg Arndt concluded that a few hundred digits of π would suffice for any scientific application. Despite this, people have diligently worked to compute π to thousands and millions of digits. With the advancement of computer technology, the competition to calculate the decimals of π has intensified. For instance, in 1949, a team led by George Reitwiesner, an American mathematician, and John von Neumann, a Hungarian-American mathematician, achieved 2,037 digits by using an inverse tangent (arctan) infinite series. This calculation took 70 hours of computer time on the ENIAC computer. Von Neumann is also well-known for his contribution to the Manhattan Project during WWII, along with Hungarian-American theoretical physicist Edward Teller and Polish-American mathematician Stanislaw Ulam.
In 2019, Emma Haruka Iwao and her colleagues at Google utilized 25 Google Cloud virtual machines to calculate 31,415,926,535,897 digits of π in 121 days.
In 2020, Timothy Mullican, a data scientist from Alabama, United States, calculated up to 50 trillion digits of π. His work earned him recognition from the Guinness Book of Records.
In 2021, a team from the University of Applied Sciences Graubünden in Switzerland calculated 62.8 trillion digits of π. The task took the team 108 days and 9 hours, making it 3.5 times faster than Mullican’s record and almost twice as fast as Google’s efforts.
3. Why is Pi So Important in Artificial Intelligence and Machine Learning?
This topic is near and dear to my heart. Let’s put it this way: without π, artificial intelligence as we know it would not exist. Here are just a few examples to illustrate this point.
π Eigenvalues.
Many of the appearances of π in the formulas of mathematics and the sciences are related to its close relationship with geometry. However, π also appears in many natural situations that seem to have nothing to do with geometry. For example, π is the smallest singular value of the derivative operator on the space of specific functions on [0, 1] that vanish at both endpoints. Lambda (λ) is an eigenvalue of the second derivative operator in the equation f''(t) = -λ*f(t).
Eigenvalues play a crucial role in Principal Component Analysis (PCA), Spectral Clustering (such as K-Means), Computer Vision, and in Gradient Descent, the cornerstone of neural networks.
π Fourier Transform
π also emerges as a pivotal spectral parameter in the Fourier transform, devised by French mathematician Jean-Baptiste Joseph Fourier. In 1807, Fourier demonstrated that any waveform could be expressed as an infinite sum of sinusoids.
The Fourier transform plays a crucial role in neural networks. Specifically, it is extensively utilized in deep learning models, including Convolutional Neural Networks (CNNs).
π The Gaussian Function
The Gaussian function, which serves as the probability density function for the normal distribution with mean μ and standard deviation σ, inherently incorporates π. Developed by the German mathematician Johann Carl Friedrich Gauss, it stands as arguably the most renowned function within the realms of statistics and probability. π represents the distinctive constant that renders the Gaussian normal distribution, expressed as exp(-πx²), equal to its own Fourier transform.
π The Cauchy Distribution
Another well-known probability density function that explicitly contains π is called the Cauchy distribution, named after the French mathematician Augustin-Louis Cauchy. Unlike the Gaussian function and other probability models under the Central Limit Theorem, the Cauchy distribution lacks finite moments of order greater than or equal to one, and it does not possess a moment generating function. This characteristic renders the Cauchy formula particularly useful for analytical modeling in fields that deal with infinite exponential growth.
π Number Theory
Euler’s results in infinite series led to a significant Number Theory finding: the probability of two random numbers being relatively prime (that is, having no shared factors) is equal to 6/π². Number Theory was utilized in the development of early machine learning models to create pattern recognition algorithms.
4. My Take
I hope I’ve convinced you that Pi (π) is the most significant constant in mathematics, science, and machine learning.
I mentioned numerous legendary mathematicians and scientists. Yet, I would add one more name to this illustrious list: my father, Viktor Polevikov. In my mind, he rightfully stands among these luminaries. He is one of history’s leading scientists in thermodynamics and magnetic fluids. In each of his research papers, he thoughtfully builds upon the foundational work of many great mathematicians who came before him—from Euler’s equations to Langevin’s Law—using their theories as launching pads to construct innovative new models. These models have been widely adopted across diverse industries, including space exploration, healthcare, finance, and energy. I’m incredibly proud of my father and the profound impact of his scientific contributions.
👉👉👉👉👉 Hi! My name is Sergei Polevikov. I’m an AI researcher and a healthcare AI startup founder. In my newsletter ‘AI Health Uncut,’ I combine my knowledge of AI models with my unique skills in analyzing the financial health of digital health companies. Why “Uncut”? Because I never sugarcoat or filter the hard truth. I don’t play games, I don’t work for anyone, and therefore, with your support, I produce the most original, the most unbiased, the most unapologetic research in AI, innovation, and healthcare. Thank you for your support of my work. You’re part of a vibrant community of healthcare AI enthusiasts! Your engagement matters. 🙏🙏🙏🙏🙏